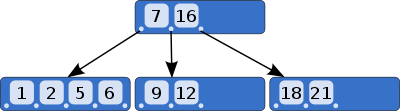
AVL 트리와 같은 균형 트리(Balanced Tree)이다.

B Tree는 자식을 두 개만 가지는 이진 트리의 단점을 보완할 수 있다.

  

균형 트리로는 AVL트리, 2-3 트리, 2-3-4 트리 등이 있다.

B Tree를 이해하면 2-3트리, 2-3-4 트리의 원리를 쉽게 이해할 수 있다.

데이터베이스들은 매우 많은 데이터를 포함한다는 점에서 B Tree 구조를 채택하고 있다.

- 자식의 개수가 많아질수록 추가적으로 소모되는 메모리 용량이 많다.

- 자식의 개수가 많아질수록 빠르게 데이터에 접근할 가능성이 높다.(높이가 낮아짐)

B Tree는 AVL 트리와 같은 균형 트리(Balanced Tree)이다.

B Tree는 삽입 및 삭제 이후에도 균형 트리를 유지할 수 있다.

B Tree는 자식을 두 개만 가지는 이진 트리의 단점을 보완할 수 있다.

- 노드의 데이터 수가 최대 N이라면, 자식의 수는 N+1이다.

- 각 노드의 데이터는 정렬된 상태이다.

- 리프 노드(Leaf Node)는 모두 같은 레벨에 있으므로 완전한 균형 트리 형태를 유지한다.

- 특정한 데이터의 왼쪽 서브 트리는 해당 데이터보다 작으며, 오른쪽 서브 트리는 해당 데이터보다 크다.

- 루트(Root) 노드가 자식을 가질 때는 최소한 2개 이상의 자식을 가진다.

- 루트(Root)와 리프(Leaf) 노드를 제외한 노드는 최소한 {(차수) / 2개}의 올림 만큼의 자식을 가지고 있다.

- 데이터 중복이 없다고 가정

탐색은 일반적인 방식, 즉 이진 탐색 트리와 동일한 방식으로 수행된다. 루트에서 시작하여, 하향식으로 탐색 대상의 값을 구분 값과 비교하며 자식 포인터를 찾아나가는 과정으로 진행한다.

부적절한 상태에 있는 노드란, 그 노드에 허용된 자식 노드의 숫자가 허용된 범위 밖인 노드를 의미한다.

1. 삽입될 노드가 어느 위치로 삽입될지 찾아 해당 부모 노드에 삽입한다.

2. 부적절한 상태의 노드가 없다면, 삽입 과정을 종료한다.

3. 만약, 어떤 노드가 너무 많은 항목을 가지고 있다면, 이를 두 노드로 분리한다. 이 과정을 반복적으로 트리를 타고               올라가며 진행한다. 만약 루트 노드를 분리하였다면, 새로운 루트 노드를 만든다.